My MSc. Thesis Journey
In this post, I’ll be talking about my thesis, based on this article, titled “A conflict free branch and bound approach for scheduling AGVs in ACTs”. This article is an important contribution to AGV-related problems because:
- the assumed path layout is bidirectional AND it aims to avoid congestion and conflict.
- The number of vertical parallel shortcuts (\(X_R\)) is very many! (in contrast to this) I will be using xpress for solving the model and GAMS’ C++ API for formulating and implementing the B&B approach.
In this page, I will store whatever I think is useful for my defense and thesis needs.
Useful websites:
- cool article about Branch and Bound’s concept in xpress’s website: https://www.fico.com/fico-xpress-optimization/docs/dms2019-03/solver/optimizer/HTML/chapter4_sec_section4003.html
- GAMS’s reference for using Xpress in it: https://www.gams.com/28/docs/S_XPRESS.html#XPRESS_USAGE
- FICO’s website, stating the solver uses b&b for solving MIP Here
- For copying gams into cmake: here
- In regard to GAMS 25.1 MIP implementation: here and also this
- This is how you might wanna define this set:
\(\boldsymbol{O(i, j, k) = \{(i,j,k)|\,\,\forall(i,j) \in c, \,\, k\in a\}}\)
in GAMS:1 2 3 4 5
set i "set of all" / i1*i12 /; set j /j1/; set a /1,2,3,4/; set c(i,j) /#i.j/; set o /#c.#a/;
- NVIDIA CUDA
- It seems that according to this article, there are more conflicts types, namely: deadlocks and livelocks (it’s good to read the review article for this purpose)
Gams related topics:
Tutorial and useful links:
- Multi-Dimensional Sets
- Comments in Gams: for putting an eol comment, you need to set
$onEolComat the start and then use!!to put eol comments. For a whole line comment, asterisk*. Note that this syntax is only used for EOL, i.e. the lines containing code, not blank lines. For inserting comments on a blank line, use*. - It seems that changing a set, e.g. union of two sets, is not allowed in gams as easily as it might seem. For this purpose, you need to define dynamic sets! (read more about them here). This is how you might have union:
1 2 3 4 5
set i /i1*i3/; set j /j1*j3/; set k; k(i) = yes; k(j) = yes;
- Assignments and data maipulation
- MIP in GAMS, including binary variables
- The
displaystatement - GDX data exchange format
- the
.and#operator (note that.might indicate Cartisian Product if used with()). if it is used out ofsetoperations, it would mean member accessing operator. - writing equations in gams
- xpress solver integration in gams
.gdxis the database file format of GAMS.- Just use the damn
gams25UG.pdffile, reserved words. And remember this code snippet: (stupid language!!!!)1
eq_1(i,j) $(not sameas(i,'i1')).. 1 =e= 1;
GAMSis not case sensitive!- Very important: You CANNOT put so-called endogenous expressions (the ones containing decision variables) inside
$()conditionals. You need to write them with$ifthenor defining auxiliary variables and intermediatory constraints. - You cannot use
$conditionals right after=e=, =l=, =g=etc. - To use solver-specific commands, read these two: GAMS docs and stackoverflow and for solver usage and for gurobi option in Gams
- To use solver-specific commands and options, you need a
.optfile, containing all the the additional options (in the link I provided somewhere in this post from GAMS website). To create and add the.optfile to your prefered solver, you need to add the following GAMS to the bottom of your code:1 2 3 4
*$onEcho > CFS.opt *iis 1 *$offEcho *ConflictFreeSch.Optfile = 1;
- Regarding Neos-server.org: if want to add some options to your solver, upload an option file to the server.
- For Detecting conflicting constraints in your model: You can iis option of the gurobi solver.
- For using indicator constraints, refer to this Gams Page and this stackoverflow answer
- For submitting job through a python client app, you need to make an XML file, read this: https://neos-server.org/neos/solvers/milp:Gurobi/GAMS-help.html
- How to Use GAMS database
.gdxwith data merge: Use$LoadDCMafter$gdxIn. Also remember that for reflecting the changes into the newest version of the data file, you need to use statements, without$, since they are used in the compile time.
The AGV Dispatching Conflict-free Article
Enough prerequisites, let’s delve into the this article:
A branch-and-bound approach for AGV dispatching and routing problems in automated container terminals [doi: https://doi.org/10.1016/j.cie.2022.107968]
- Note that time limit in the article for gurobi is 3600 seconds.
- Also, Handover Points (HPs) do exist both in quay side and yard side.
Some important assumptions
The AGV cannot turn multiple times in the seaside and landside operation areas. This means than AGV cannot change horizontal lanes once it is in the seaside (\(y \in \{1,\dots, y_r\}\quad \text{or}\,\,\,\, y \in \{ y_{r+1}, \dots, y_R\}\)). HENCE this is where horizontal confilict occurs, since or else, the AGV would change lane if there is an AGV on the front when doing horizontal action!
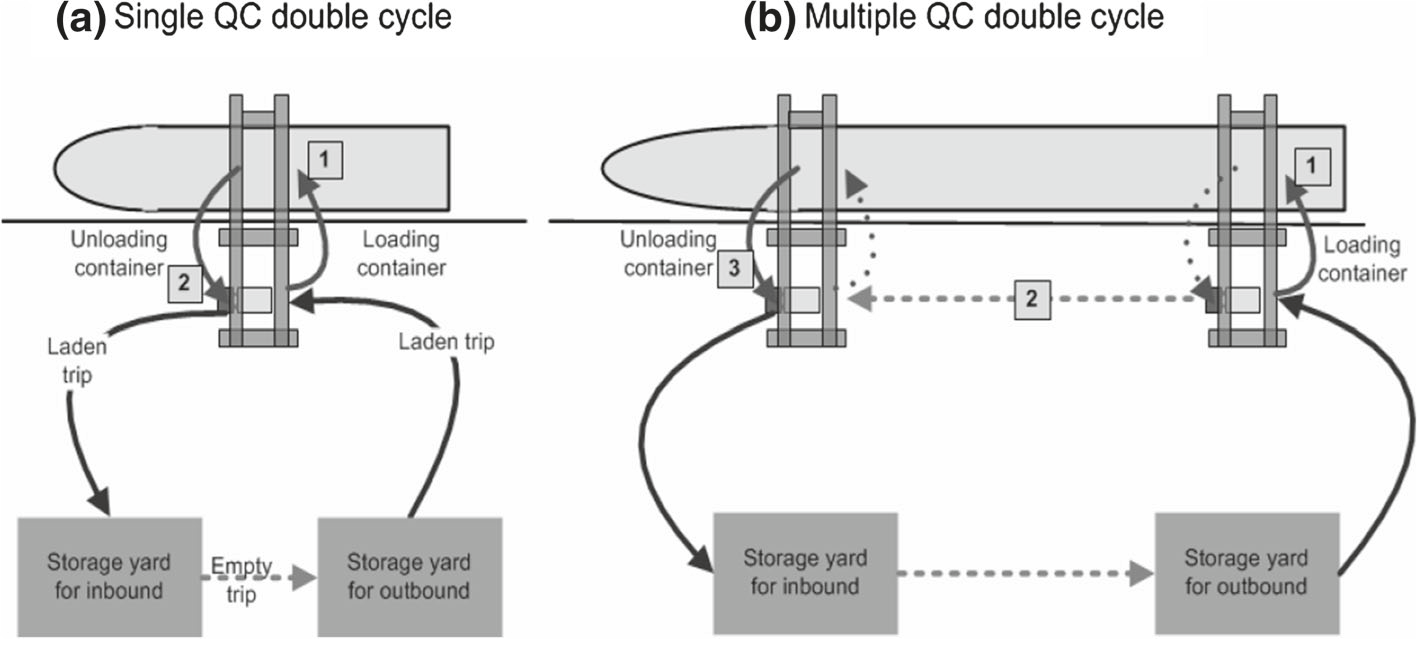
Multiple QC double cycling: In this model, the sequence (or consecutive) task of loading and unloading is NOT performed by a single QC but by two QCs consecutively with the use of a single vehicle. (shown in b) Note that in multiple QC double cycling model, QCs can perform empty container handling.
Parameters:
So 3 types of parameters and sets are used:
Common parameters:
These are common parameters used in AGV VRP problems:
- \(\boldsymbol{v_{AGV}}\) (constant AGV speed = 4m/s), \(\boldsymbol{m}\) (the index of QCs), \(\boldsymbol{i}\) (index of i-th job of QCs), \(\boldsymbol{\alpha}\) (index of AGV actions)
- The traveling speed of QCs (not the trolley speed) is 2.7 Km/h.
Action and Container sets:
- Container Sets: \(\boldsymbol{C_L, C_D}\) (set of loading and unloading containers), \(\boldsymbol{C = C_L \cup C_D}\) is a two dimensional set of \(\boldsymbol{C = \{(m,i), m \in m, i \in i \}}\)
- Horizontal and Vertical Action sets: \(\boldsymbol{W^V}\), \(\boldsymbol{W^H}\) (set of vertical (Horizontal) AGV Actions, \(\boldsymbol{\alpha}\) = \(2\)(\(1,3,4\))) Note: as the starting location and the destination (storage location) of each container is pre-determined, these two sets need to be written according to these locations!
Port Layout parameters:
These involve AGV paths:
- parameters are: \(\boldsymbol{x_R}\) (width of agv op), \(\boldsymbol{y_r}\) last vertical Landside Area, \(\boldsymbol{y_R}\) last Seaside Area, \(\boldsymbol{l}\) (the index of AGVs)
- \(Y^S\) (seaside vertical paths), \(Y^L\) (landside vertical paths), \(X^R\) (Horizontal paths)
Port Specific parameters:
- \(\boldsymbol{O_{(m,i)} \in X^R}\) :location of Containers on the ship:
- For L container: \(o_{(m,i)}\) means the location of the loading container on the ship
- For D container: \(o_{(m,i)}\) means the starting location of an unloading container on the ship. Therefore: \(o_{(m,i)}\) is strictly related to ships.
- \(\boldsymbol{\psi _1, \psi _2}\) QC and ASC op schema (used in 30 and 31 const). These parameters are strictly related to the stowage plan of the port (containers on higher tiers are unloaded first while those on lower tiers are loaded first!). These two sets also ensure the sequence of loadings and unloadings into the ship.
Important note: Bays could be assigned to multiple QCs (read this) But I do not consider it! (hence \(m=n\))- Note that:
- For a QC or ACS, if the container is being discharged, (Tier of (m,i)) \(\ge\) (Tier of (n,j))
- For a QC or ACS, if the container is being loaded, (Tier of (m,i)) \(\le\) (Tier of (n,j))
- Note that:
- \(A_L(m,i)\) and \(A_R(m,i)\): right-most and left-most path of the block storing the containers:
- For an L container: its right-most and left-most path of its starting block location.
- For a D container: The destination (the storage location) which is determined by someone (I just picked a random number between 1-6).
Time related parameters:
- \(\boldsymbol{G^Q_{(m,i)}}\) (required time for QC to op \(\boldsymbol{(m,i)}\)),
- \(\boldsymbol{G^Y_{(m,i)}}\) (required time for AGV to op \(\boldsymbol{(m,i)}\) onto AGV-supp),
- \(\boldsymbol{S^Q_{(m,i),(m,i+1)}}\) (required time for QC switch) Used for QC-double cycling model.
Decision Variables:
Conflict related Variables
- \(\boldsymbol{Z_{(m,i)(n,j)l}}\): it’s mostly concerned with consecutive operation of AGVs \(\rightarrow\) AGV job assignemnt and container allocation. Note that \((m,i) \ne (n,j)\)
- \(\boldsymbol{U^{AGV}_{(m,i,\alpha_1)(n,j,\alpha_2)}}\): if \((m,i,\alpha_1) \prec (n,j,\alpha_2)\) (conducted before). Note that \((m,i,\alpha_1) \ne (n,j, \alpha_2)\).
This variable clarifies the sequence of two different actions conducted, taking care of when one action starts so that it wouldn’t be in conflict with another one. (mostly it deals with the those three situations in Fig 6. of the article.) - \(\boldsymbol{U^{QC}_{(m,i)(n,j,\alpha)}}\): if Cont (\(m,i\)) of QC is conducted before H Act of (\(n,j,\alpha\))
Path and Location Variables:
Location Variables:
- \(P^X_{(m,i,\alpha),x}\) if Finish of \((m,i,\alpha)\) is on \(x\)
- \(P^Y_{(m,i,\alpha),y}\) if Finish of \((m,i,\alpha)\) is on \(y\)
Start Var:
- \(P^X_{(m,i, 0),x}\) if Finish of \((m,i)\) is on \(x\)
- \(P^Y_{(m,i, 0),y}\) if Finish of \((m,i)\) is on \(y\)
Time vairables:
- \(\boldsymbol{T^Q_{(m,i)}}\) Start of QC Op on (m,i)
- \(\boldsymbol{T^Y_{(m,i)}}\) Start of AGV of putting (m,i) on ASCs
- \(\boldsymbol{T^{start}_{(m,i,\alpha)}}\): start of AGV to conduct act \((m,i,\alpha)\)
Auxiliary variables
These can be written in terms of each other.
- \(\boldsymbol{t^{\text{AGV}}_{(m,i,\alpha_1)(n,j,\alpha_2)}}\) shows long it takes for \((n,j,a2)\) for be completed.
\(= \Big( \Big| X^{\text{position}}_{(m,i,\alpha_1)} - X^{\text{position}}_{(n,j,\alpha_2)} \Big| + \Big| Y^{\text{position}}_{(m,i,\alpha_1)} - Y^{\text{position}}_{(n,j,\alpha_2)} \Big| \Big) \Big/ v^{\text{AGV}}\)
OR
\(t^{AGV}_{(m,i,\alpha_1)(n,j,\alpha_2)} = \frac{\Delta x+ \Delta y}{v^{AGV}}\) - \(\boldsymbol{X^{\text{position}}_{(m,i,\alpha)}}\): finishing location of \(\boldsymbol{(m,i,\alpha)}\)
- \(\boldsymbol{Y^{\text{position}}_{(m,i,\alpha)}}\) finishing location of \(\boldsymbol{(m,i,\alpha)}\)
Constraints in GAMS
Important note: Firstly, remember that the symbols in front of the article constraints are the ones appearing in the indices of the constraints of the GAMS. take look at the example below:
\(\sum_{l \in B} \sum_{(n,j) \in C \cup \{0\} } Z_{(m,i)(n,j),l} = 1, \,\, \forall(m,i) \in C\)
1
cnstr_2(m,i) $(C(m,i) and not sameas(m,'m0') and not sameas(i,'i0')).. sum((li,n,j) $(C(n,j)), z(m,i,n,j,li)) =e= 1;
some constraints, for example, \(\boldsymbol{eq_2((m,i))}\) take as its counter, the (m,i), but we can’t set (m,i) as the counter, ‘cause it’s 2-dimensional. However, we might handle it with ord(C(m,i))… idk.
Very important part of the article
- Read 6.1 of the Article, very important notes about the value of some parameters (parameter estimation) and Instance Generation (Our Data) This part is concerned with many of the values of parameters, such as \(\boldsymbol{v_{AGV}}, S^Q_{(m,i)(m,i+1)}\).
Remember for \(\psi_{2}\), for \((m,i,n,j)\) being a member of it, \((m,i)\) and \((n,j)\) need to belong to the same block in the Yard side and ASC op.
- Constraint 8 in the article could be written as follows:
- \[P^X_{(n,j,0)} - 10^{10}(|1-\sum_{l\in B} z_{(m,i)(n,j)l}|) \le P^X_{(m,i,4)}\]
- \[P^X_{(n,j,0)} + 10^{10}(|1-\sum_{l\in B} z_{(m,i)(n,j)l}|) \ge P^X_{(m,i,4)}\]
Important note: If you want to add new container jobs to the bbapp.gms file, be sure to adjust d1, d2 and d3 in the beginning of the gms file. These denote the index of the last job of each QC.
Unanswered questions
- In fig. 1, are the unloading containers (\(\boldsymbol{(m,i) \in D}\)) stored in blocks in the ships? (if so, \(\boldsymbol{A^L_{(m,i)}, A^R_{(m,i)}}\) should contain unloading containers!)
- How are those two sets defined for unloading containers as the layout of containers in the ships are different from the storage area?
Does \(O_{(m,i)}\) map \((m,i)\) to only one value? because the m-th QC moves to different blocks of the ship it is operating on… (At least that’t what seems logical to be the case!!)
- Did you know that the below constraint clarifies the relationship between decision variable \(P^X_{(m,i,\alpha),x}\) and \(t^{AGV}_{(m,i,\alpha_1)(n,j,\alpha_2)}\)? However, take note of this constraint:
Problem: both \(t^{AGV}_{(m,i,\alpha_1)(n,j,\alpha_2)}\) and \(P^X_{(m,i,\alpha),x}\) are here!
- What the hell is the definition of \(S_{(m,i)}\) and \(R_{(m,i)}\) in the definition of the upper bound algorithm? What is the set of operation time for each container? – Answer: \(R(m,i)\) is a subset of \(W_T\). Each route for container \((m,i)\) is a bunch of actions taken by the \((m,i)\).
- How to determine whether assignment of container (m,i) to agv l is compatible with \(\psi_1,\psi_2\)??
Deficiencies of the base article
- The schedule for which container should be dispatched to where is known. WHY??? As I’ve understood, the container i-th is known to where is should be sent (whether it being a QC or a block in the Storage area). So, the problem of container allocation to QC or Blocks remains open! (Could be related to integrated scheduling).
- If with respect to 3. in unanswered questions, \(O_{(m,i)}\) is set to just one value, then the problem of scheduling QC container jobs for block placement on the ships is not considered, which is not cool! We could add a variable denoting allowed positions of qc for its i-th container!
- Number of blocks on the ship and the number of ships are not considered!
- The speed of AGV is constant. Why can’t it accelerate?? What would happen if it does?
- This article has overlooked the AGV charging constraints according to this
- As the article considers the block location of the stored unloading containers, we need to have a grasp of how many ships there are and how many blocks each has (on average), which is overlooked in the article!
- The article does not take into account the Horizontal movement of QCs. S_Q must be modified then!
- what is the distribution of loading and unloading jobs?
- Sensitivity analysis for
G_QsndG_Y, since they follow normal distibutionsU(30,60)
Implementation of the Article
Data structures:
- Set AGVs B (objects):
- Stack of assigned containers
- The time for completing each job.
- Set of QCs m (objects)
- list (stack) of a QC’s operations \(i_m\)
- Set of containers C: (m,i)
- set of unassigned containers \(C'\)
- set of horizontal paths \(Y_R\)
- set of Vertical paths \(X_R\)
- Set Schemes P for distributing jobs to AGVs:
- list of horizontal actions WH(m,i,(a1,a3,a4))
- list of vertical actions WV(m,i,(a2))
- Linked list of \(\psi_1(m,i,n,j)\) and \(\psi_2(m,i,n,j)\), showing the ordering of jobs (for \(\psi_1(m,i,n,j)\), both \((m,i)\) and \((n,j)\) belong to the same QC op list and (for \(\psi_2(m,i,n,j)\), both \((m,i)\) and \((n,j)\) belong to the same Block)
- Set \(N_\tau\): set of nodes in level \(\tau\)
- \(\tau\) the height
- node \(v\)
- \(C_{\tau, v}\) and \(C'_{\tau, v}\), containers assigned and to be assigned
- Node \(v\): (according to LB model of the paper)
- \(b_l\) number of unassigned containers to AGV \(l\)
- \(t_v^{min}\), shortest op time for unassigned container set \(C'_{\tau ', v}\)
- \(Z'_{(n,j),(m,i),l}\) sequence of two containers assigned to the same AGV. cf. \(Z_{(n,j),(m,i),l}\). We have relaxed the “immediately conducted” constraint!
- \(t_{(m,i)}\) Min time for AGV conducting \((m,i)\) Without considering conflict (WCC):
\(\sum_{l\in B} \sum_{(n,j)\in C\cup {0}} t_v^{min}.b_l.Z'_{(n,j),(m,i),l}\quad \forall (m,i)\in C_{\tau ', v}\) - \(t^{empty}_{(m,i),(n,j)}\) constant
- \(t^{load}_(m,i)\) constant
- Scheme set \(P\) depending on parameter \(q\), the maximum number of containers assigned to each AGV with respect to the inequality below: (\(t^{min}\) should relate to \(S_{(m,i)}\)) \(q.t^{min} \le T^{UB}\)
- set of possible routes for container \((m,i)\) denoted as \(R_{(m,i)}\) and the set of its op time, sorted from smallest to largest \(S_{(m,i)}\).
Important Questions:
- How to implement “multiple double cycling verifier”? This is done through updating \(Z_{l,(m,i),(n,j)}\) and checking whether cnstr_6 and cnstr_7 hold or not!
- How to implement ”\(\psi_1\) and \(\psi_2\) compatibility verifier”?. This seems easy!
In order to write constraints in CPP, you need to associate your defined custom types (Quaycranes, AGVs, Containers) with the decision variables of the article. For example, for decision variable \(Z_{l,(m,i),(n,j)}\) we might need something like std::vector<tuple<AGV, Container, Container, bool>> z;
Sensitivity Analysis:
cnstr_19can be used to set which block, the D container in QC side can be stored!
TODO
- Job Generator:
- \(W_H\) and \(W_V\) of each container should be written according to destination location.
- \(psi_1\) and \(psi_2\) should be rewritten according to QC and ASC Op Scheme
- \(o_{m,i}\) in
BBAPP2.gmsneeds modification, according to parameters definition.
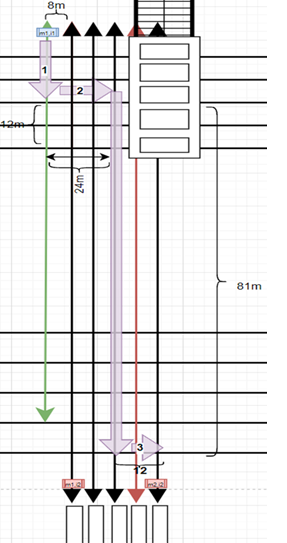
- \(S_{(m,i)}\) and \(R_{(m,i)}\): An example of computing distance and actions 1,2,3 is given below:
- How to determine whether the assignment of container (m,i) to agv l is compatible with \(\psi_1,\psi_2\)??